Micro-tidal disruption events of stars

The Sun is an isolated, single star that evolves in a more-or-less predictable fashion. However, many stars in our Universe live in very dense stellar environments like globular clusters which alters their lives. In the cores of such clusters, the density of stars can exceed 10⁵ that of the Solar neighbourhood. This significantly increases the chance of dynamical encounters between stars and other objects, such as black holes, in cluster cores.

We explored these encounters between low-mass stars (like the Sun) and stellar-mass black holes, whose masses are 5-100 times that of the Sun [paper]. To achieve this, we used the 3D hydrodynamics code AREPO and the 1D stellar evolution code MESA. If the closest approach distance r_p is comparable to the star-black hole system's tidal radius r_t, the star can get tidally disrupted, with two streams of matter escaping the star on either side. An even closer approach can result in the star being completely destroyed. These are called 'micro' tidal disruption events or μTDEs to distinguish them from TDEs due to supermassive black holes. Studying μTDEs is important because they change the remnant star's future evolution and trajectory, result in accretion of matter on to the black hole, and can thereby affect the dynamics of the host cluster.

The following interactive buttons provide animations of μTDEs of large range of input parameters. Note: For m_★ = 0.5 M_⊙ stars, we only ran simulations with H_c = 0.70.

Dynamical stability of multiple-star systems

Additional complexity in the evolution of stars can arise from the presence of companion stars. The Sun is a single star and is not representative of the vast array of stellar systems that dwell in our Universe. More than half of these stars, especially massive stars of masses greater than 10 times that of the Sun, have one or more companions. Thus, our night sky is brimming with binaries (2 stars), triples (3 stars), quadruples (4 stars) and more.

Binary-star systems are dynamically stable and follow closed orbits forever, at least in the regime of Newtonian dynamics and point masses. When a third star is added (the famous three-body problem), the stellar orbits can become chaotic resulting in the escape of one of the stars. Nevertheless, we do observe triples, quadruples and higher order multiples, implying that they can remain gravitationally bound for a very long time given a certain configuration. This stable configuration is a hierarchy, where stars are arranged in 'nested' binaries. For example, a hierarchical triple comprises an 'inner' binary of two relatively close stars, and an 'outer' binary made up of a distant third star and the center of mass of the two inner stars.

Animations of hierarchical multiple-star systems are shown below. The python3 scripts for these animations are available on my GitHub repository multiple-stars-animation.

Using machine learning and the N-body code MSTAR, we systematically analyzed the dynamical stability and instability of triples [paper 1] and quadruples [paper 2]. In the case of triples, the 6 parameters which stability depends on include the inner and outer mass rations q_in = m₂/m₁ and q_out = m₃/(m₁+m₂), the semimajor axis ratio α = a_in/a_out, the inner and outer eccentricities e_in and e_out, and the mutual inclination i_mut between the two orbits. We did not consider the dependence on other orbital angles. Similarly, for 2+2 and 3+1 quadruples, we looked at the dependencies on 11 equaivalent parameters (three mass ratios, two semimajor axis ratios, three eccentricites and three mutual inclinations). We then employed a neural network to classify triples and quadruples residing in these multi-dimensional parameter spaces as 'stable' or 'unstable'. These classifiers are freely available on my GitHub repositories triple-stability and quadruple-stability.

Future: Await web tool for interactive classification!

Gravitational waves in quadruple-star systems

Apart from gravitational dynamics and tides, binary-star (and higher order) systems can have matter interactions. When two stars are close enough that one of the stars fills its gravitational Roche lobe, it can transfer mass onto its companion. This Roche lobe overflow (RLOF) occurs either when a star expands due to stellar evolution or the orbit shrinks (or both). When RLOF becomes unstable, the lost mass can surround the two stars, resulting in a common envelope (CE) evolution. Illustrations of RLOF and CE are shown below.

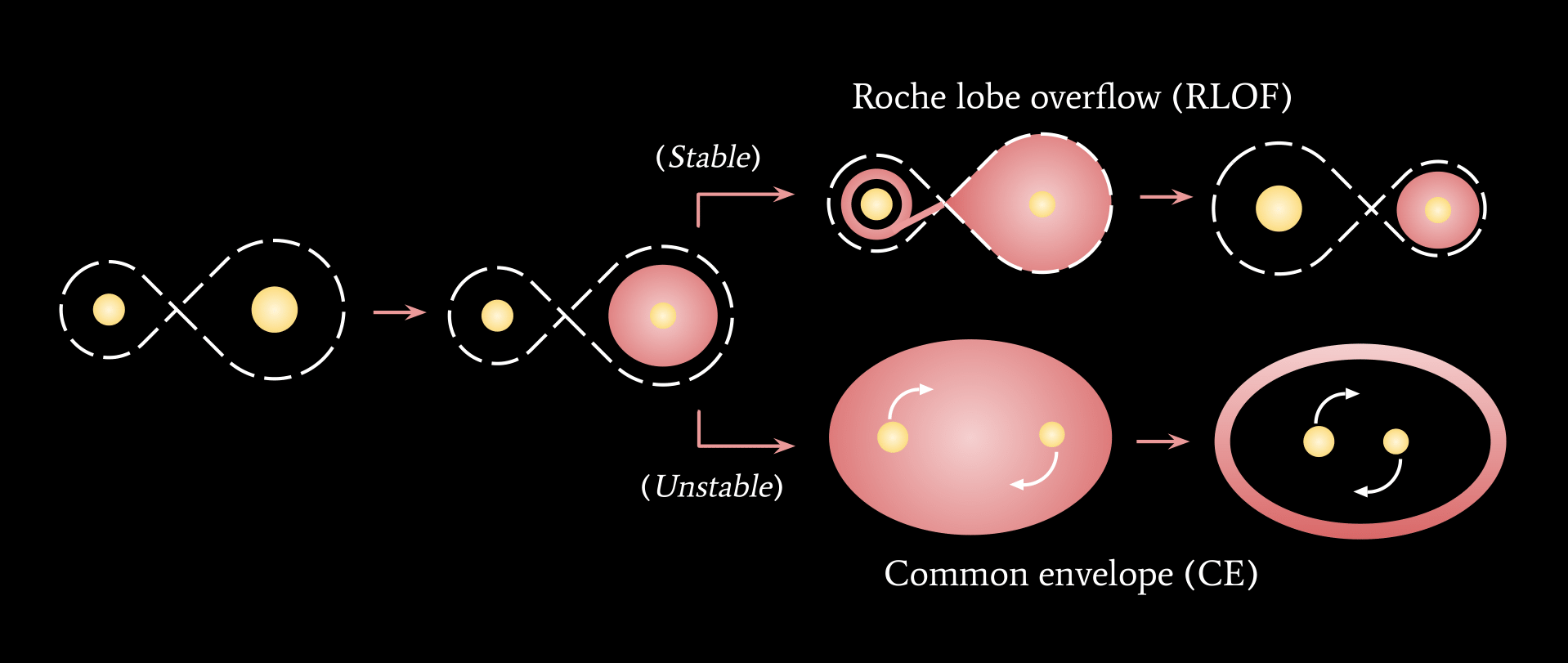
Mass transfer enables the stars to come much closer to each other due to friction, which is crucial in the context of mergers of compact objects like neutron stars and black holes within the age of our Universe. These compact object mergers cause ripples in space-time, termed gravitational waves. Massive stars (with masses greater than approximately 10 times that of the Sun) are instrumental to gravitational wave emission as neutron star and black hole are the end products of their stellar evolution. Finally, since massive stars are predominantly found in triples and quadruples, it is critical to study their evolution in detail. Moreover, the intricate dynamics of such systems can bring stars closer together faster, potentially enhancing the number of compact object mergers.

To that end, we conducted a population synthesis study, using the code MSE, to estimate the occurance of such mergers in quadruple-star systems [paper]. Using MSE with realistic intial conditions, we evolved hundreds of thousands of 2+2 and 3+1 quadruple-star systems from birth to death. We found that a small, but significant, fraction of these systems result in the formation of binary compact objects that merge within the age of our Universe. In addition, we found the detectable rates of gravitational wave events from quadruple-star systems to be similar to those from binary-star systems, thereby underscoring their importance.

Other short projects

• Comparison of real and simulated galaxies using Deep Learning [PDF]
• Study of low frequency Quasi-Periodic Oscillations in accreting black hole binaries[PDF]
• Identification of Young Stellar Objects using Spitzer archive data [PDF]
• Verification of star clusters using Colour-Magnitude Diagrams [PDF]